Scientists develop second sound theory

4 July 2019

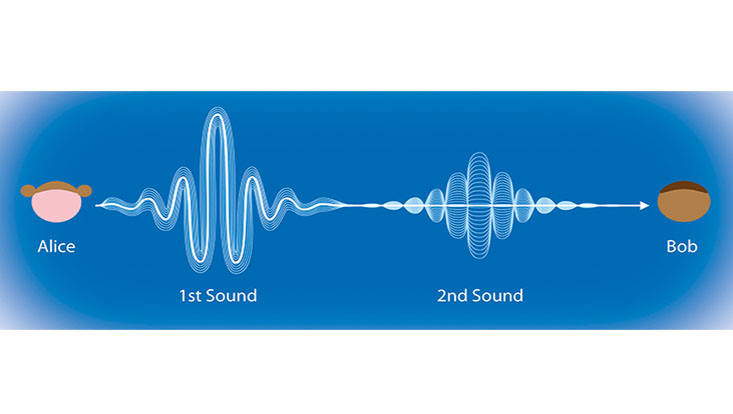
Photo: UHH, Mathey group

In quantum liquids there is a special phenomenon: In addition to normal sound propagation there is a second sound.

Sound moves at different speeds depending on whether it passes through air, water or another liquid. In superfluid helium, it can even be heard twice: as second sound. A team of scientists led by Prof. Ludwig Mathey from the cluster of excellence “CUI: Advanced Imaging of Matter” at Universität Hamburg has presented a new theory in the journal "Physical Review A" that captures the second sound in quantum liquids.

Sound travels faster in water than in air, checking in at 1493 meters per second, on a summer day of 25°C. Other liquids have their own sound velocity: alcohol, for example, 1144 meters per second, helium 180 meters per second in the liquefied state, which is reached at a temperature of -269°C.

If we cool down that helium to more than -270°C, it turns into a quantum liquid, a superfluid that flows without friction. In this state, the sound would be heard twice. While the first sound moves in superfluid helium at 250 meters per second, the second sound has a speed of 25 meters per second.

“For superfluid helium, second sound is slower than first sound”, explains co-author Vijay Singh. In order to capture the phenomenon of the second sound in quantum liquids, a new theoretical approach was necessary.

“We generalized the Feynman path integral to expand the theory of superfluids,” describes lead author Ilias Seifie the conceptual advance. While the Feynman path integral formulates quantum mechanics as a sum over trajectories, these trajectories themselves are classical. A classic trajectory is, for example, the path of a billiard ball, where you can see the location and speed.

With quantum mechanical particles, however, there are uncertainties, because sometimes, for example, the location cannot be determined exactly and is smeared over a certain range. “We modified the classic trajectories so that they contain information about quantum fluctuations,” continues Seifie.

The first sound still corresponds to a normal trajectory, which for example deviates from the vibrating string of an instrument. The cross-section of this curve usually has a more or less constant diameter along its entire length (see Figure 1). Since the particle resistance in a quantum fluid is lower and the sound waves also expand in width, the expansion of the curve varies. This is how the second sound is produced.

The formula of the new path integral therefore also covers shapes in which the cross-section varies and, for example, assumes an elliptical shape as if the curve were squeezed. Fittingly, physicists refer to these quantum mechanical states as squeezed states.

Mathey: “This approach is widely applicable. It can be applied to any method that is based on path integrals.” Many phenomena at the interface of quantum and classical physics can be better understood with this approach, by restructuring the Feynman path integral, for example superconductivity. Text: CUI

 Citation:

Vijay Singh, Ilias Seifie, Ludwig Mathey

"Squeezed-field path-integral description of second sound in Bose-Einstein condensates"

Phys. Rev. A 100, 013602 – Published 1 July 2019

DOI: 10.1103/PhysRevA.100.013602